Chaos-Theorie und seltsame Attraktoren
Der Butterfly Attractor
Dieser Text hat rein gar nichts mit Fotografie zu tun, nicht mal im entferntesten. Er soll zeigen, dass man mit einfachsten Mitteln der Mathematik ästhetisch ansprechende Bilder erzeugen kann. Und das verbindet dann doch wieder mit der Fotografie.
Es geht um Chaos. Nicht um das Chaos, welches auf meinem Schreibtisch herrscht, sondern um deterministisches Chaos. Deterministisches Chaos ist ein mittlerweile fest etablierter Begriff der Mathematik und Physik, der von dem Mathematiker James A. Yorke geprägt wurde und im wesentlichen folgendes beinhaltet:
Deterministisches Chaos beschreibt das irregulär erscheinende chaotische Verhalten eines Systems, das seinerseits aber von streng deterministischen dynamischen Gesetzen beherrscht wird. Das Chaos wird also nicht durch äußere Umstände verursacht, sondern ist dem System immanent.
Bei dem System kann es sich ein physikalisches Doppelpendel, das Wetter oder die Populationszahlen von Raub- und deren Beutetieren handeln (Populationsdynamik). Mit anderen Worten: deterministisches Chaos tritt bei vielen natürlichen und künstlichen Systemen auf. Die meisten Systeme in unserer täglichen Umwelt sind chaotisch, wir bemerken es nur nicht immer. Außerdem verhalten sich auch Systeme, die chaotisch sein können, mitunter regulär.
Unter welchen Bedingungen entsteht nun deterministisches Chaos? Zunächst einmal muss das System nichtlinear sein. Aus der Schulmathematik erinnert man sich vielleicht an die Begriffe lineare Gleichung (y=a*x+b) und quadratische Gleichung (y=a*x2+b*x+c). Und das beschreibt stark vereinfacht auch schon das Wesen von Nichtlinearität: ein lineares System wird ausschließlich durch lineare Gleichungen, ein nichtlineares System durch quadratische Gleichungen oder solche höheren Grades beschrieben.
Des weiteren muss das System das zeigen, was man in der Fachsprache als “sensible Abhängigkeit von den Anfangsbedingungen” bezeichnet. Was ist darunter zu verstehen? Wenn man einen Ball mit einer bestimmten Anfangsgeschwindigkeit unter einem bestimmten Winkel wirft, wird er an einem bestimmten Ort ankommen. Verändert man die Anfangsgeschwindigkeit nur geringfügig, wird der Ball, wie zu erwarten, an einem geringfügig anderen Ort ankommen. Gleiche Ursachen erzeugen gleiche Wirkungen, ähnliche Ursachen erzeugen ähnliche Wirkungen. Ein chaotisches System hingegen wird, so geringfügig die Unterschiede in den Anfangsbedingungen auch sein mögen, an völlig verschiedenen Orten akommen. Gleiche Ursachen erzeugen immer noch gleiche Wirkungen (sonst wäre es kein deterministisches System), ähnliche Ursachen erzeugen aber nicht (!) mehr ähnliche Wirkungen.
Gerade diese Eigenschaft chaotischer Systeme ist bis heute nicht in das Bewusstsein der Allgemeinheit vorgedrungen. Die meisten Menschen sind dem linearen Denken verhaftet, insbesondere auch jene, die es von Berufs wegen besser wissen sollten. Ein chaotisches System, welches mit zwei unterschiedlichen Anfangsbedingungen gestartet wird, landet nach einer hinreichend langen Zeit in Zuständen, die scheinbar nichts mehr miteinander zu tun haben, auch wenn die Unterschiede in den Anfangsbedingungen nur in der hundersten oder tausendsten Stelle nach dem Komma lagen. Chaotische Systeme sind gewissermaßen die Substantiierung des Spruchs “Kleine Ursache – große Wirkung”. Der berühmte, im Zusammenhang mit Chaos geprägte Satz “Der Flügelschlag eines Schmetterlings in China kann Tage später einen Wirbelsturm in Florida auslösen” deutet auf die chaotische Natur des Wettergeschehens hin. Und das ist auch der Grund dafür, dass es aus prinzipiellen Gründen niemals möglich sein wird, langfristige Wettervorhersagen über Wochen oder Monate zu erstellen.
Vorarbeiten zur Chaostheorie wurden schon im 19.Jahrhundert von Poincaré geleistet, der eigentliche Anfang geht aber zurück in die sechziger Jahre des vergangenen Jahrhunderts, als der Meteorologe Edward Lorenz ein einfaches System von Gleichungen untersuchte, die die zeitliche Entwicklung des Wetters beschreiben. Er fand dabei den jetzt nach ihm benannten Lorentz-Attraktor. Heute ist deterministisches Chaos ein fest etabliertes Teilgebiet der Mathematik und Physik geworden, und nachdem die anfängliche Euphorie, mit Chaos alles erklären zu können, verflogen war, wandte man sich ernsthaften und praktischen Dingen zu. Inzwischen ist die Chaostheorie Grundlage vieler moderner technischer Errungenschaften.
Faszinierend sind die “nutzlosen” Seiten der Chaostheorie allemal, sind mit ihrer Hilfe doch ästhetisch ansprechende Bilder von fragiler Schönheit auf einfachste Weise zu erzeugen. Das in den achtziger Jahren des vergangenen Jahrhunderts auf Schritt und Tritt anzutreffende Apfelmännchen (eine sog. Mandelbrot-Menge) gehört ebenso dazu wie der Lorenz-Attraktor oder eine einfache, zweidimensionale diskrete Abbildung, der sog. Hénon-Attraktor. Als ich selbst damals ein wenig mit Chaos experimentierte, fand ich Mitte der achtziger Jahre ein chaotisches Gebilde, welches meines Wissens bis dahin noch nicht beschrieben war und welches ich “Butterfly attractor” nannte (nicht zu verwechseln mit dem berühmten Lorenz-Attraktor).
Folgende einfache mathematische Iterationsvorschrift
xn+1 = yn + 1 – a * exp(-xn2)
yn+1 = b * xn
erzeugt bei bestimmten Parameterwerten a und b einen seltsamen Attraktor, die typische Ausprägung chaotischen Verhaltens. Seltsame Attraktoren sind gewissermaßen die Ordnung im Chaos, die Orte, an denen sich all die chaotisch erzeugten Punkte versammeln. Bei verschiedenen Parameterwerten ergeben sich zum Teil völlig unterschiedliche Bilder, von denen nachfolgend einige zu sehen sind.



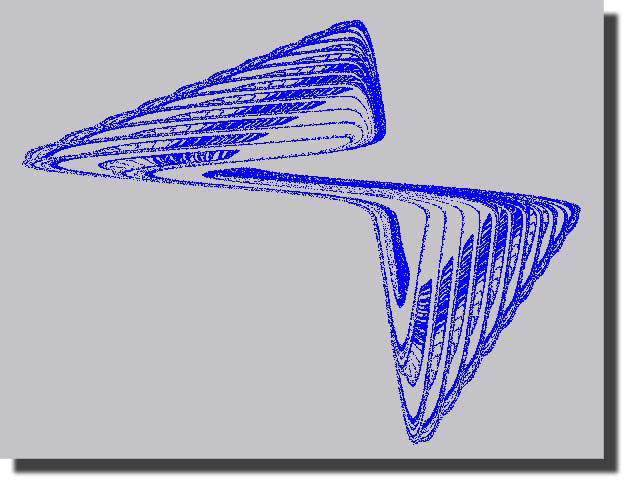
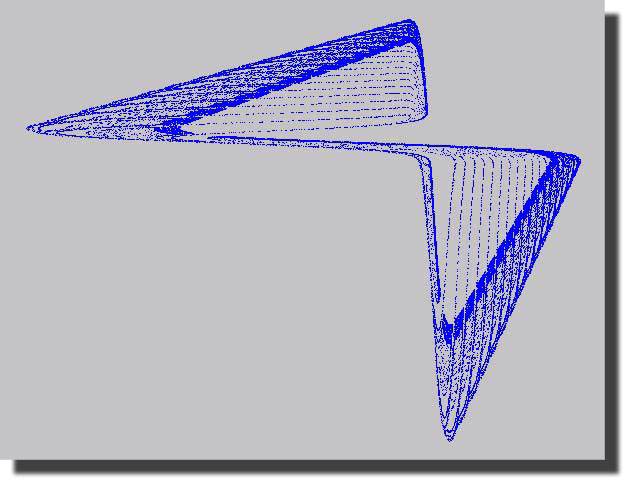
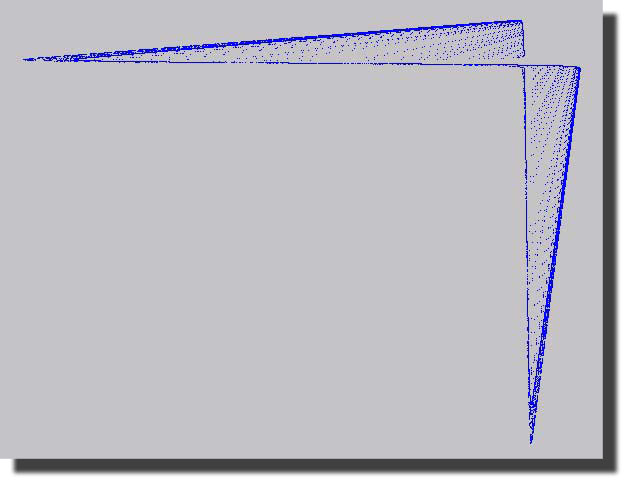
Bei Werten a <= 3 ergeben sich ziemlich “langweilige” Bilder, das System verharrt dann in einigen wenigen sog. Fixpunkten. Fixpunkte sind isolierte Punkte, die sich unter der Iteration nicht verändern.
Interessant ist folgende Tatsache: ganz gleich, welchen Startpunkt man wählt, ergibt sich visuell immer dasselbe Bild. Der Startpunkt wird gewissermaßen von dem sich schließlich ergebenden Bild “angezogen”, woraus sich auch der Name “seltsamer Attraktor” erklärt. Man kann dies leicht ausprobieren, indem man unterschiedliche Startpunkte (x- und y-Werte) eingibt. Und noch eines kann man leicht demonstrieren: die empfindliche Abhängigkeit von den Anfangsbedingungen. Man starte einmal mit zwei Punkten, die sich beispielsweise erst in der sechsten Stelle nach dem Komma unterscheiden. Visuell erhält man dasselbe Bild, aber die beiden sich beispielsweise nach 5000 Iterationen ergebenden Punkte liegen an völlig unterschiedlichen Positionen. Man kann also voraussagen, welche Zustände das chaotische System annehmen wird, d.h. welches Bild sich ergibt, aber man kann nicht voraussagen, wann das System welchen Zustand einnimmt.
Mit Hilfe eines modernen PCs sind diese Abbildungen in Sekundenschnelle erzeugt, damals in den 1980ern dauerte es noch mehrere Minuten. Wer sich für die mathematischen Hintergründe interessiert und selbst ein wenig experimentieren möchte, der kann sich hier das entsprechende Mathcad-Script (Mathcad ist ein exzellentes Programm, mit dem man numerische/symbolische Mathematik betreiben kann) oder die zugehörige PDF-Datei herunterladen.

